[전자회로] 라자비 전자회로 razavi

Miller's Theorem $밀러효과$

 

Folating Impedance를 접지된 2개의 impedance로 변환 시키는 방법을 밀러 효과 라고 하며, Folating Impedance가 캐패시터인 경우 각 노드에 하나의 극점으로 연관시키도록 하는 방법이다.

 

이러한 Flotaing Impednace는 input impedance를 낮추고 output Impedance를 높이는 효과가 있다.

 

이를 사용하는 이유는 

 

위 처럼 캐패시터가 양단에 걸려 있으며 이를 Folating Cap이라고 하는데 만약 이러한 캐패시터가 접지가 되어있다면 극점$pole$을 통한 bandwith이를 예측 할 수 있기에 바닥에 접지하는 방법에대해서 사용할려고 Miller' theorem을 사용한다.

 

 

 

$$\frac{V_{1}-V_{2}}{Z_{F}}\;=\;\frac{V_{1}}{Z_{1}}\\ \frac{V_{1}-V_{2}}{Z_{F}}=-\frac{V_{2}}{Z_{F}}$$

 

$$Z_{1}= Z_{F}\times \frac{V_{1}}{V_{1}-V_{2}}= \frac{1}{1-A_{v}}$$

 

$$Z_{2}= Z_{F}\times \frac{-V_{2}}{V_{1}-V_{2}}= \frac{Z_{F}}{1-\frac{1}{A_{v}}}$$

 

$$A_{v}=-A_{0}$$

 

$$Z_{1}=\frac{1}{(1+{A_{0}})C_{Fs}}$$

 

$$Z_{2}=\frac{1}{(1+{\frac{1}{A_{0}}})C_{Fs}}$$

 

Applying to Floating Cap w/ inverting Circuit

 

 

$$Z_{1}=\frac{1}{(1+{A_{0}})C_{Fs}}$$

 

$$Z_{2}=\frac{1}{(1+{\frac{1}{A_{0}}})C_{Fs}}$$

 

이러한 수식을 통해 Z1의 경우 input impedance 관점에서 gain$A0$에 의해 입력임피던스가 낮아짐을 확인 할 수 있다. 역으로 Z2의 경우는 gain이 커질수록 output impedance가 커짐을 확인 할 수 있다. 

 

Example

 

$$C_{in}=(1+A_{0})C_{F}=(1+gmR_{D})C_{F}\\C_{out}=(1+\frac{1}{gmR_{D}})C_{F}$$

 

RC cap -> CR cap

 

 

$$\frac{V_{out}}{V_{in}}(s)=\frac{R_{1}}{R_{1}+\frac{1}{C_{1}s}}=\frac{R_{1}C_{1}s}{\sqrt{R_{1}C_{1}s+1}}\\\\\left| \frac{V_{out}}{V_{in}}\right|=\frac{R_{1}C_{1}w}{\sqrt{R_{1}^{2}C_{1}^{2}w_{1}^{2}}+1}$$

 

RC 순서와 반대로 CR 순서대로 연결되어진 경우 pole 기점 까지 증가하는 경향이 있다.

 

Example)

 

Ci는 coupling cap$직류는 차단하고 교류는 넘겨주는$으로 앞서 말한 CR순서로 연결되어져 있기 때문에 

$2\pi \times 20Hz = \frac{1}{R_{1}C_{i}}\to C_{i}=80nF \uparrow$ 이다 여기서 Ci가 만약 80nF보다 작다면 Hz값은 20Hz보다 증가하게 될 것이고 그럼 20Hz이하의 signal을 전달하지 못하기 때문에 80nF보다는 커야한다.

 

$2\pi \times 20k = \frac{1}{\frac{1}{gm}C_{L}} \to  C_{L}\;=\;40nF\downarrow$ 뒷 부분에 CL은 40nF이 나오게 되고 만약 이 값보다 크다면 20KHz이상의 signal 영역에 대해서 전달하지 못하기 때문에 40nF보다는 작아야한다

 

$$C_{L}\leq 40nF \\ C_{i}\geq 80nF$$

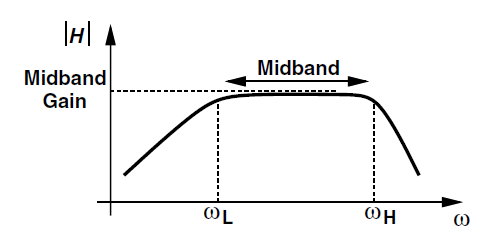
그래서 회로는 $w_{L}$ 와  $w_{H}$ 사이의 Midband range가 있고 그 영역 사이에서만 유효한 gain을 전달하는 Midband Gain이 존재한다. 

 

Capacitor Components in MOSFET

 

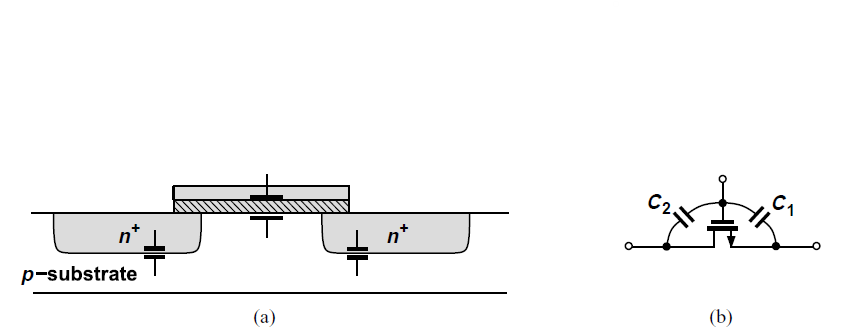
이전까지는 mosfet 외부에 capacitor에 대해서 많이 학습하였다 하지만 mosfet 내부에서도 capacitor를 필수적으로 고려해줘야한다. 

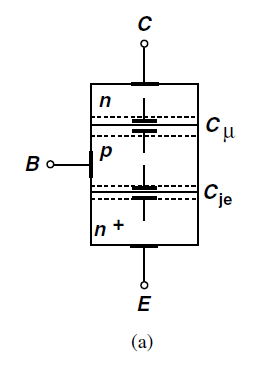
앞선 설명해서 n과 p 사이의 depletion reigon이 존재하고 이는 도체 절연체 도체를 나타내는 capacitor 같은 역할을 보인다.  그래서 p-n jucncton이 바로 cap이다. 

 

그래서 1개의 MosFet에는 총 4개의 Capacitor로 생각 할 수 있는데 $C_{GS}\;\;C_{GD}\;\;C_{SB}\;\;C_{DB}$

 

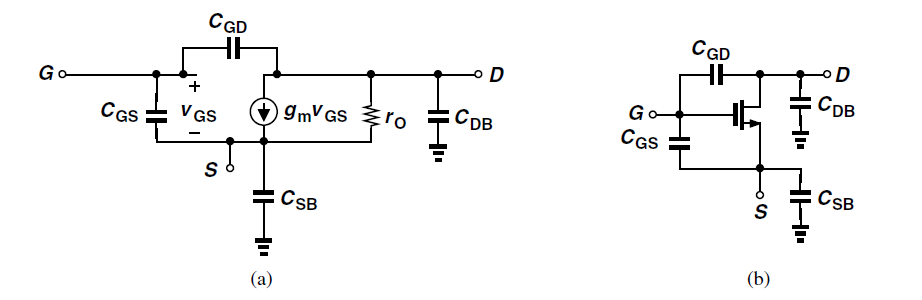
small siganl model에서 고려하면 위 그림처럼 나타 낼 수 있다.

 

 

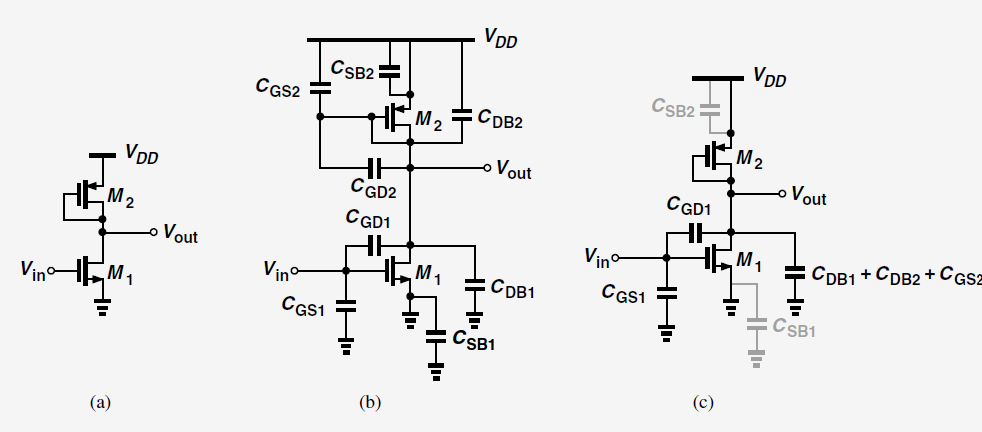
그림 a를 통해 두개의 Mosfet에 대한 존재를 확인했고 b에서 각각 4개의 capacitor를 확인 할 수 있다.  

$$M_{1}\;\;\rightarrow \;\; C_{GS1}, \;C_{SB1}, \;C_{DB1}, \;C_{GD1}\\M_{2}\;\;\rightarrow \;\;C_{GD2},\;C_{GS2},\;C_{SB2},\;C_{DB2}$$

 

캐패시터는 양단의 전압차가 존재하지 않을때 short 되므로 $C_{SB1},\;C_{GD2},\;C_{SB2}$는 short 처리한다.

 

나머지 캐패시터에 대해서 작성해주고 $C_{DB1}+C_{DB2}+C_{GS2}$는 한 도선에 연결되어져 있으므로 다 더해줘서 표현할 수 있다