Scalar : magnitude (크기) ex 길이 온도 전압 무게 속도
Vector : magnitude (크기 +) & 방향 ex) 속도, 힘, 전기장, 자기장
Inner produc
$$\vec{a}\cdot \vec{b}=\left| a\right|\left|b\right|cos\theta =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$$

Proof) 이를 증명해 본다면, 코사인 2법칙
$$c^{2}=\left|a \right|^{2}+\left|b \right|^{2}-2\left|a \right|\left|b \right|cos\gamma\\ (\vec{a}-\vec{b})^{2}=(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+(a_{3}+b_{3})^{2}-2\vec{a}\bullet \vec{b}\\\vec{a}\bullet \vec{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$$
$$\left|a\bullet b \right|=\left| a\right|\left|b \right|\left| cos\gamma \right|\leq \left|a \right|\left| b\right|\;\;(Couchy-Schwahz\;inequality)$$
$$\left| a+b\right|^{2}=(a+b)(a+b)=\left| a\right|^{2}+\left|b \right|^{2}\pm 2a\bullet b\leq \left| a\right|^{2}+\left|b \right|^{2}\pm 2\left|a \right|\left| b\right|=(\left| a\right|\pm \left| b\right|)^{2}\\\left|a+b \right|\leq \left| a\right|+\left| b\right|$$
Projection of the vector
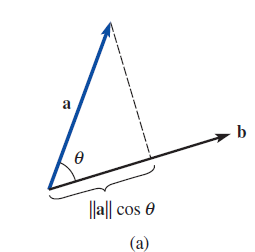
$$\left| a\right|cos\theta =\frac{a\bullet b}{\left|b \right|}=a\hat{n}$$
b vector에 정사영한 a를 확인하기 위해서는 a의 크기의 절대값에 a와 b사이의 cos값을 곱해주면 된다 a와b의 내적공식의 cos을 통해서 정리할 수 있고 이는 a의 방향벡터에 b의 단위벡터를 곱한 값으로 나온다.
example) work done by a forece

$$W=\left|f \right|cos\theta \left| d\right|=\vec{f}\vec{d}$$
자기 모멘트의 포텐셜 에너지
$$V=-\vec{m}\bullet \vec{B}$$
자기장과 자석의 내적의 음수를 곱한것이 포텐셜 에너지 이다. 최소의 값은 cos값이 1일때 최소의 값 즉, 같은 방향일때 최소의 값을 같게되고 cos값이 180도 일때 최대의 값을 갖게 된다. 포텐셜 에너지가 항상 낮은쪽으로 갈려고 하기 때문에 나침판같은 예시를 생각해보면 항상 자기장 방향으로 가르킨다.
Line as a vector
$$a_{1}x+a_{2}y=0\;\;\leftrightarrow\;\;\vec{a}\bullet \vec{b}=0\\\vec{r}=(x,y)\;\;{\color{Blue} \\ \vec{a}=(a_{1},a_{2})\;\; normal\; vector}$$
원점을 지나는 직선내의 한점 (x,y)를 잡는다면 그 방향의 법선벡터는 a1,a2 라고 표현 할 수 있다. 여기서 평행한 직선
$${\color{DarkGreen} a_{1}x+a_{2}y=c}\to \vec{a}\bullet \vec{b}=C\Leftrightarrow \hat{a}\bullet \vec{r}=\frac{c}{\left|a \right|}$$
원점으로부터 평행한 직선 까지의 거리는 x,y로 표시할 수 있고 이와 방향벡터 a의 내적은 직선과의 최단 거리 즉, 사영한 거리가 나오게 되고 이는 c를 법선벡터의 크기로 나눈 값이 된다.
In 3d 3차원 공간에 $\vec{a}\bullet \vec{r}=C$ 는 a라는 법선벡터에 대한 평면을 의미한다. a라는 방향을 가진 벡터에다가 원점에서 그 평면을 가르키는 벡터를 r벡터라 한다면, 이를 a에 사영한 값이 같은 길이를 의미한다.
$$\frac{\vec{a}}{\left|a \right|}\bullet \vec{r}=\frac{c}{\left| a\right|}\\\hat{n}\vec{r}=\frac{c}{\left|a \right|}$$
이러한 형태를 Hess's nomal form 이라한다.
Cross Product

\vec{v}=\vec{a}\times \vec{b}

Triple scalar product

이 공식에 대한 의미를 살펴보자면
$\left| \vec{b}\times \vec{c}\right|$는 방향은 평면의 법선방향이면서 평행사변형의 넓이를 나타낸다.
$\left| a\right|cos\theta $는 그 법선방향의 크기 a만큼을 사영한 것으로 즉 입체도형의 높이를 나타내는 것을 의미한다
이를 곱하면 입체도형의 넓이를 알 수 있다.