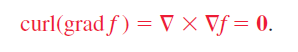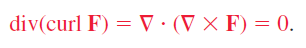Gradient of a scalar filed
스카랑장에 대한 미분을 Gradient로 정의 할 수 있
$$D_{b}f=\hat{b}\bullet \triangledown f=\left| \hat{b}\right|\left| \triangledown f\right|cos\gamma \leq \left| \triangledown f\right|$$
이번에는 함수의 기울기 즉, 방향성에 대해서 볼 것이다. 각 함수의 x,y,z의 위치에 따른 변화는 미분으로 표현될 수 있다.
방향벡터 r에 대해서 이를 적용해 본다면, $ f(\vec{r}+d\vec{r})-f(\vec{r})=df\\ =f(x+dx,y+dy,z+dz)-f(x,y,z)\\=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz$ 로 정의할 수 있다.
여기서 f(x+dx)-f(x)는 f'(x)dx로 표시 할 수 있는데 이는 테일러 급수 정리를 통해서 표현 할 수 있다.
Directional derivative (편미분) 방향벡터로의 미분
1차원 공간에서는 방향이 정해져 있기때문에 고려 하지 않아도 되었지만 3차원 공간에서는 여러가지 방향이 존재하기 때문에 이에 대한 방향성에 대해서도 고려해줘야하는데 이를 Directional derivative라고 한다. 어떤 r벡터를 b방향으로의 미분을 하게 되면,
$$D_{b}f=\displaystyle \lim_{\delta \to 0}\frac{f(\vec{r}+\delta \hat{b})-f(\vec{r})}{\delta }=\displaystyle \lim_{\delta \to 0}\frac{\triangledown f\times \delta \hat{b}}{\delta }=\hat{b}\triangledown f$$
b방향으로의 편미분을 했다는 것은 함수 f에 대해서 gradient 후 b 방향의로의 방향성을 곱해주면 된다.
Gradient direction of maximum increase
기울기의 최대 증가량을 구하기 위해서는
$$D_{b}f=\hat{b}\triangledown f=\left|\hat{b} \right|\left|\triangledown f \right|cos\gamma \leq \left|\triangledown f \right|$$
여기서 최대 증가량은 gradient f이다. 다만 cos값이 최대값 1 이기 위해서는 방향벡터 b와 f가 평행해야한다. 여기서 알 수있는 것은 gradinet f는 좌표평면을 어떻게 잡더라도 그 값이 일정하게 때문에 독립이라고 말 할 수 있다.
tangent palne은 접 평면을 의미하는데, 어떠한 일정한 점에 접하는 미소평면을 확대한 개념이라고 생각하면 된다.
이 평면위의 좁은 영역에서의 벡터 공간들의 편미분 값은 0 이여야 한다. 왜냐하면 f(x,y,z)=c라는 스칼라 영역에서의 변화율이 존재하지 않는 평면을 형성했기 때문이다. 즉, 이는 방향벡터 b와 함수 f가 서로 직교한다는 것을 의미한다.
이에 대한 Example 을 풀어보면 $F(x,y,z)=\frac{1}{2}x^{2}+\frac{1}{2}y^{2}-z+4\Rightarrow \triangledown F=xi+yj-k\\ \triangledown F(1,-1,5)=i-j-k\\(x+1)-(y-1)-(z-5)=0\Leftrightarrow -x+y+z=7$
1,-1,5에서의 법 평면을 구하기 위해서는 일단 함수 F에 대해서 정리해야한다. 함수 F(x,y,z)를 정리하기 위해서 각 x,y,z방향으로의 미분을 하고 그 해당하는 점을 대입해주면 법평면을 구할 수 있다. 이 법평면을 점 (1,-1,5)에 해당하는 평면을 만들어주면, 위와같이 정리 할 수 있다.
* Application
1. Force-potentail
$$\vec{F}=-\triangledown f\\ \phi (r)=\frac{1}{4\pi \varepsilon }\frac{Q}{r}=\frac{c}{r}\\ -\triangledown \phi =-C\left [ \frac{\partial }{\partial x}\frac{1}{r},\frac{\partial }{\partial y}\frac{1}{r},\frac{\partial }{\partial z}\frac{1}{r}\right ]=\frac{c}{r^{3}}\left [ x,y,z\right ]=\frac{c}{r^{3}}\vec{r}=\frac{c}{r^{2}}\hat{r}\;\;\;(r=\sqrt{x^{2}+y^{2}+z^{2}})$$
쿨롱포텐셜이란 대전된 물체들이 접근하면 극성의 전기는 반발하고 다른 극성의 전기는 끌어들이는 힘을 쿨롱의 힘이라고 한다. 이러한 쿨롱의 힘을 통해서 gradient를 행해주면, 전기장을 구할 수 있다. 즉, 어떤 방향 r로 향하는 전기장에 대한 식을 정리할 수 있다.
Divergence of a vector field
$$div\;\vec{V}=\vec{\triangledown }\vec{V}\\ (\frac{\partial }{\partial x}i,\frac{\partial }{\partial y}j,\frac{\partial }{\partial z}k)\bullet (v_{1}i,v_{2}j,v_{3}k)\\\frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y}+\frac{\partial }{\partial z}v_{3}\to sclar\;field$$
발산(Divergence)란 임의의 공간에서 벡터장이 퍼져나오는지 혹은 모이는지를 크기로 나타낸 것을 의미한다.
또는 이를 벡터장의 발산이 어떤 미소면적에 대한 빠져나오는 양과 들어오는 양 즉, 단위 부피 당 유량이라고 할 수 있다.
그럼 이때 전기장에서의 Divegence에 대해서 한번 구해보겠다.
$$\vec{\triangledown }\vec{E}=c\vec{\triangledown }\cdot (\frac{x}{r^{3}},\frac{y}{r^{3}},\frac{z}{r^{3}})=0$$
전기장에서의 발산은 원점을 제외한 모든 구간에서 0 이다 즉 전하가 없는 위치에서 발산은 없다.
$$\vec{\triangledown }\vec{E}=-\vec{\triangledown }\vec{\triangledown }\phi =-(\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}+\frac{\partial^2 }{\partial z^2})\phi =-\triangledown ^{2}\phi \;\;Laplacian\\ \triangledown \bullet E=0\Leftrightarrow \triangledown ^{2}\phi=0 \;Laplace \;\;equation$$
전기장은 사실 쿨롱의 힘을 div 취한것을 통해서 얻어낸 것인데 이를 통해서 Laplacia 방정식을 유도할 수 있다.
Curl of a vector field
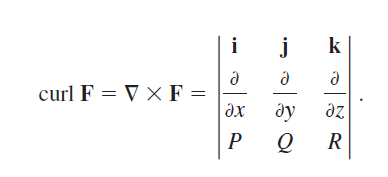
$$=(\frac{\partial v_{3}}{\partial y}-\frac{\partial v_{2}}{\partial z})i+(\frac{\partial v_{1}}{\partial z}-\frac{\partial v_{3}}{\partial x})j+(\frac{\partial v_{2}}{\partial x}-\frac{\partial v_{1}}{\partial y})k$$
curl 은 회전하는 것을 나타내는 기호이다 이를 이전 전기장에서 사용한 공식을 사용하면
$$E=-\triangledown \phi \to \triangledown \times E=0$$
즉, 보존장은 회전하지 않는다는 것을 의미한다.
