surface integrals
$$\vec{r}=(x(u,v),y(u,v),z(u,v))$$
매개변수방정식 ( parametric representation )으로 이 surface를 표현 할 수 있다 구체적인 예를 들어보면
첫번째 예시는 원통이다. 이 원통위에 좌표를 우리는 좀 더 쉽게 표현 할 수 있는데, u와 v를 통해서 우리는 원통위의 좌표를 표현 할 수 있다.
$$x^{2}+y^{2}=a^{2}\;\;\;-1\leq z\leq 1 \\\;0\leq u\leq 2\pi \;\;-1\leq v\leq 1\\ \vec{r}=(acosu,asinu,v)$$
이를 원통좌표계로도 표현이 가능한데 $(\rho,\; \phi,\; z)$ 로 표현이 가능하다 여기서 rho는 반지름의 길이 phi는 회전 반경 z는 높이를 의미한다.
이번에는 구의 좌표를 표시해볼것이다. $$0\leq u\leq 2\pi \;\;-\frac{\pi }{2}\leq v\leq \frac{\pi }{2}\\ \vec{r}=(acosv\cdot cosu,acosv\cdot sinu,asinv)$$
구의 좌표를 매개변수르 이용하여 더 간단하게 표현 할 수 있는데 u를 우리는 경도 즉 longitude v를 위도 즉 latitude라고 할 수 있다. 여기서 a는 구의 반지름을 의미한다.
spherical cordinate 구면좌표계
$(r,\; \phi,\; \theta )\;0\leq \phi \leq 2\pi \;,\;0\leq \theta \leq \pi $ 라고 기술할 수 도 있다.
Tangent Plane and Surface Normal
$$\vec{N}=\vec{r_{u}}\times \vec{r_{v}}:\;\;normal\;\;vector $$
우리는 접선벡터에서 미분을 통해서 접선을 구할 수 있었다 그럼 접평면의 경우는 어떻게 구할 수 있을까? 한점 P에서 다른 두 방향의 외적을 통해서 접평면을 구 할 수 있다. 단위법선 벡터로 변경하기 위해서는
$$=\frac{\vec{r_{u}}\times \vec{r_{v}}}{\left| \vec{r_{u}}\times \vec{r_{v}}\right|}$$
If S: g(x,y,z)=0 일때 $\triangledown g\propto \vec{N}$
스칼라 필드에서 법선벡터를 구하기 위해서는 gradient를 취해주면 된다
$$du\;\Rightarrow\; \frac{\partial \vec{r}}{\partial u}du \\ dv\;\Rightarrow \;\frac{\partial \vec{r}}{\partial v}dv \\ \vec{r}_{u}du\times \vec{r}_{v}dv=\vec{N}dudv\\{\color{Blue} \vec{dA}=\hat{n}dA}$$
du의 변화가 있으면 r벡터에 u방향으로의 변화가 생기고 dv의 변화가 생기면 r벡터의 v방향으로의 변화가 생긴다.
이를 외적하게 되면 dA에 대한 벡터를 형성할 수 있다.
Flux integral
$$\int \int_{S}^{}\vec{F}\cdot d\vec{A}\;(if\;S\;is\;clsed)\\ =\int \int_{R}^{}\vec{F}(\vec{r}(u,v))\cdot (\vec{r}_{u}\times \vec{r}_{v})dudv\;(R\;domia\;in\;the\;uv\;plane)\\ \int \int_{R}^{}(F_{1}dA_{1}+F_{2}dA_{2}+F_{3}dA_{3})\\=\int \int_{S}^{}(F_{1}dydz+F_{2}dzdx+F_{3}dxdy)$$
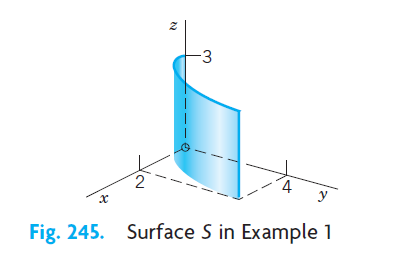
벡터 F에 대해서 곡면 S에 대한 유량을 구하기 위해서는 대표적으로 두가지 방식이 존재한다 하나는 매개변수로 변환하여 벡터 F에 대해서 법선벡터 n 의 내적을 통해서 유량을 구하는 방법이다. 법선벡터 n은 r을 u와v로 각각 미분한 것을 외적하게 되면 N벡터가 형성이 된다. F와N의 내적을 한 후 u와 v의 범위에 대해서 적분을 취해주면 값이 나온다
1)
$$S: y=x^{2}\;\;0\leq x\leq 2,\;\;0\leq z\leq 3\\ \vec{F}=(3z^{2},6,6xz)\\ \vec{r}=(u,u^{2},v)\;\;(0\leq u\leq 2,\;0\leq v\leq 3)\\\vec{N}=\vec{r}_{u}\times \vec{r}_{v}=(2u,-1,0)\\\vec{F}=(3v^{2},6,6uv)\;F\bullet N=6uv^{2}-6\\\int \int_{S}^{}F\bullet dA=\int_{0}^{3}\int_{0}^{2}(6uv^{2}-6)dudv=72$$
두번째 방법은 스칼라 f를 통해서 gradient를 취해주면 법선이 나오게 된다 그 법선을 단위법선벡터로 만들어 주고 이를 벡터 F와 내적해야한다 다만 여기서 dA 미소면적에 대해서 구해줘야하기 때문에
2)
$$f(x,y,z)=x^{2}-y=0\to S\\ \vec{n}=(2x,-1,0)\rightarrow \frac{(2x,-1,0)}{\sqrt{1+4x^{2}}}\\ \vec{F}\cdot \hat{n}=\frac{(6x^{2}-6)}{\sqrt{1+4x^{2}}$$
$$\int_{0}^{3}\int_{0}^{2}\frac{(6x^{2}-6)}{\sqrt{1+4x^{2}}}\sqrt{1+4x^{2}}dxdz$$
F벡터와 n벡터의 내적과 dA를 곱한것이다. dA의면적은 $\sqrt{x^{2}+y^{2}}=\sqrt{1+4x^{2}}dxdz$이다.
