
Feedback system을 배우는 이유는 냉장고를 예로 들면 3도를 맞추기를 희망해서 X 입력값에 온도 낮추게 한다면, 계속 낮아질 것이다 만약 3도 이하로 내려가게 된다면 이를 Feedback해줘서 유지해야하는데 이때 필요한게 Feedback system이다
X-XF=Error라고 할 수 있고 K=XF/Y를 feedback factor라고 한다.
Y=A1(X−XF)→Y=A1(X−KY)→(1+A1K)Y=A1XYX=A11+KA1
라고 정리 할 수 있는데 K가 0이 아닌 closed-loop 에서 Y/X를 통해 gain을 구하게 되면 A1에 1+KA1만큼 감소하게 된다.
Example

R2R1+R2Y→XFK=R2R1+R2YX=A11+kA1YX=A11+R2R1+R2A1
Relation between Error and X

E=X−XF→XF=A1E×K Error를 X에 대한 방정식을 세우기 위해서 위와 같이 방정식을 세웠다. Error는 X-XF이기 때문에 이를 gain에 넣고 식을 대입하면 된다. 최종적으로 E=X1+KA1 라는 식이 나오게 된다.
이식을 통해서 loop gain 이 만약 엄청나게 크다면 KA1또한 커지기 때문에 Error값은 0에 수렴하게 된다. 또한 XF가 X를 잘 카피하는 signal이라고도 할 수 있다.

여기서 만약 KA1이 엄청나게 크다면 어떻게 나올까?
YX=A11+KA1=1K→1+R1R2(K=R2R1+R2)
만약 gain이 크다면 gain과 상관없이 1+R1/R2 값이 나오게 된다. 이렇게 되면 1/K 즉 loop gain이 굉장히 중요한 parameter가 된다.
Loop gain

앞서 봤듯이 Loop gain은 Feedback system 에서 중요한 parmeter로 작용한다는 것을 알 수 있었다. 일반적인 system에서 loopgain을 구하는 방법에 대해서 살펴보면
1. 먼저 loop를 끊은 후 2. input X를 ground처리한다. 3. test input을 연결해주고 4. output을 측정한다.
VN=KVtest×A1→VNVtest=−KA1
Feedback을 쓰는 이유

YX=A11+KA1
XFY=R2R1+R2
YX=A11+R2R1+R2A1(A1≫1)=1+R1R2
YX=4R1R2=3
R2R1+R2=14→YX=A11+14A1A1=1000YX=3.984A1=500YX=3.968
A1의 값이 1000과 A1의 값이 500에서 gain의 값의 차이가 거의 없다 즉, feedback system을 통해서 일관된 gain을 얻을 수 있다.
System become less sensitive
gain의 값은 많이 줄지만 그 값에 대한 안정성 및 bandwith의 증가 덕분에 일관된 gain을 얻을 수 있기떄문에 이점이 크다.
pole을 통해서 bandwith구간이 얼마나 extention 됬는지를 확인해 보자면
A1(s)=A01+sw0
YX=A01+sw01+KA01+sw0→A01+w0+KA0→A01+KA01+w01+KA0Bandwith=(1+KA0)w0

unity−gainbandwith란gain이1인주파수0dB일때의주파수를의미
YX(w)=A01+KA01+jw(1+KA0)w0|A01+KA0√1+w2(1+KA0)w20|=1
(A01+KA0)2=1+w2h(1+KA0)w20A20w20−(1+KA0)w20=w2h=w20A20(1−K2)=wh=w0A0
wh에 대해서 풀면된다 1+KA가 >>1크기 때문에 1을 생략한 KA값만 나오게 되고 K의2승이 <<1작기 때문에 지워질 수 있다.
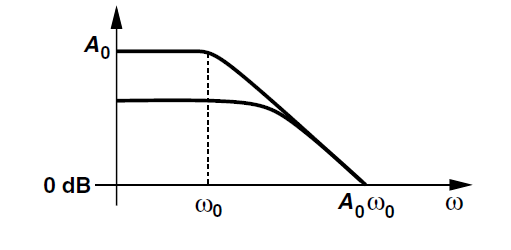
최종적인 그림은 위와 같다 원래 pole 보다는 A0배 만큼 더 먼 곳에서 pole이 생기고 bandwith또한 길어졌다. 다만 gain은 줄어들었다
'전자공학' 카테고리의 다른 글
| [전자회로] 8장 Op amp 0 | 2024.09.13 |
|---|---|
| [전자회로] 라자비 Frequency Response of Cascode Stage & Differential Pair 2 | 2024.07.21 |
| [전자회로] 라자비 전자회로 Razavi 0장 Amplifier 0 | 2024.07.07 |


